树链剖分 学习笔记
树你应该懂的吧o( ̄︶ ̄)o
学习树链剖分之前需要先学习:$dfs$、线段树(当然大佬们用树状数组代替线段树也可以O(∩_∩)O),据说一名普及+的$oier$应该都会呀
先来了解树链剖分的用处
已知一棵包含$N$个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
如果直接暴力的话,肯定会TLE(废话)。所以这时候,树链剖分闪亮登场。
什么是树链剖分
一种算法(废话),它通过分轻重边把树分割成很多链,然后利用某种数据结构维护这些链(比如上文提到的线段树、树状数组等)但前提是这种数据结构支持动态修改(你别给我整个RMQ)。本质上是一种暴力算法。
PS:树剖的复杂度约为$O(nlog^2n)$
树链剖分的基本概念
| 名称 | 概念 |
|---|---|
| 重儿子 | 父亲节点的所有儿子中子节点数目最多(sz最大)的节点 |
| 轻儿子 | 父亲节点除了重儿子以外的儿子 |
| 重边 | 父亲节点和重儿子连成的边 |
| 轻边 | 父亲节点和轻儿子连成的边 |
| 重链 | 由多条重边连成的路径 |
| 轻链 | 由多条轻边连成的路径 |
没看懂?没关系,结合下面这张图:(红色的边代表重边,黑色的边代表轻边,红色的节点代表重儿子,黑色的节点代表轻儿子)
PS:这里默认树根也是重儿子。
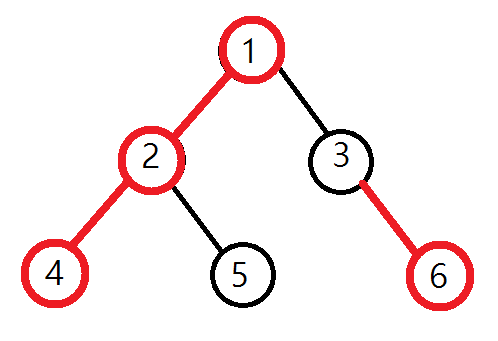
上图的重链有:1-4,3-6。
变量声明
1 | ll fir[MAXN],nxt[MAXN*2],son[MAXN*2],w[MAXN*2],tot; |
| 名称 | 作用 |
|---|---|
| $fir_x$ | 关于$x$的最后一条边编号 |
| $nxt_x$ | 关于$x$的上一条边编号 |
| $son_x$ | 第$x$条边的连向 |
| $w_x$ | 其实没啥用,打着习惯了 |
| $a_x.ls$ | 编号为$x$的节点的左儿子 |
| $a_x.rs$ | 编号为$x$的节点的右儿子 |
| $fa_x$ | 编号为$x$的节点的父亲 |
| $c_x$ | 编号为$x$的节点的重儿子 |
| $rk_x$ | 当前$dfs$标号在树中所对应的节点的编号 |
| $top_x$ | 编号为$x$的节点所在链的顶端节点编号 |
| $id_x$ | 编号为$x$的节点$dfs$后的新编号 |
| $dep_x$ | 编号为$x$的节点的深度 |
| $sz_x$ | 以编号为$x$的节点为根的子树的节点个数 |
树链剖分的实现
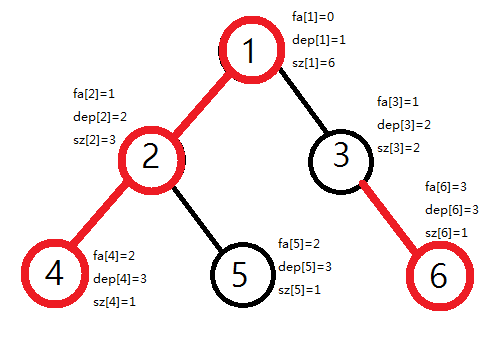
第一次$dfs$求出每个节点的重儿子、父亲、深度、子树大小。
PS:如果一个点的多个儿子所在子树大小相等且最大,那随便找一个当做它的重儿子就好了,叶节点没有重儿子,非叶节点有且只有一个重儿子。
1 | inline void dfs1(ll x,ll f,ll deep){ |
操作完以后应该是下图:
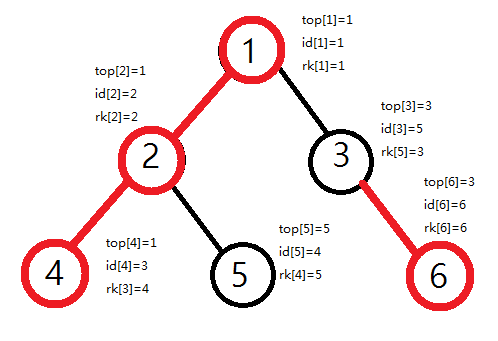
第二次$dfs$求出每个节点的链顶端节点、新编号、$dfs$编号对应的节点编号。
1 | inline void dfs2(ll x,ll ttop){ |
操作完以后应该是下图:
线段树等数据结构的维护
接下来就是线段树、树状数组等数据结构的维护了,具体使用哪种数据结构因题目而异,这里提供模板题(上文介绍的题目)所使用的线段树(区间修改、区间询问)。
1 | inline void pushup(ll x){ |
根据题目需要添加操作
就比如上文的题目中还要求的操作:
- 操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
- 操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
与操作3、操作4不同,这里要求的是一条路径上的节点,而没有告诉我们节点的编号,所以,我们这时要求出节点编号:
1 | inline ll Query(ll x,ll y){ |
当然,还有一个操作是非常常用的,那就是求lca(最近公共祖先)。
1 | inline ll lca(ll x,ll y){ |
模板题代码
对对对,就是上文提到的题目。
1 | #include<bits/stdc++.h> |
完美撒花✿✿ヽ(°▽°)ノ✿
博弈论之威佐夫博弈 学习笔记
博弈论之威佐夫博弈
威佐夫博弈(Wythoff’s game)是指的这样一个问题:有两堆各若干个物品,两个人轮流从任意一堆中取出至少一个或者同时从两堆中取出同样多的物品,规定每次至少取一个,至多不限,最后取光者胜利。
——转自百度百科
就比如洛谷的P2252 取石子游戏就是威佐夫博弈的裸题。。。
威佐夫博弈的性质
首先,由题目可知,当这两堆石子一样多时,先手获胜;当有一堆石子为空时,先手获胜。
现,我们设$(a[i],b[i])$表示先手必败的局势,其中$a[i],b[i]$分别表示两堆石子的个数。我们又称这种局势为奇异局势。
那么,我们就可以推出一些较小的数据的必败局势(奇异局势):
假如说这两堆石子的初始状态为(1,2)。那么则有如下几种情况:
(1)先手从第一堆中取一个,后手从第二堆中取两个,先手输,后手赢。
(2)先手从第二堆中取一个,后手将两堆都取一个,先手输,后手赢。
(3)先手从第二堆中取两个,后手从第一堆中取一个,先手输,后手赢。
(4)先手从两堆中各取一个,后手从第二堆中取一个,先手输,后手赢。
通过推理石子状态为(1,2)的所有可能,我们可以发现石子状态为(1,2)时,先手必输(双方都采用最优策略)。
在此,我就不列举其他奇异局势的推理过程。现将奇异局势的表单贴下来:
| 个数 | 状态 |
|---|---|
| 1 | (0,0) |
| 2 | (1,2) |
| 3 | (3,5) |
| 4 | (4,7) |
| 5 | (6,10) |
| 6 | (8,13) |
| 7 | (9,15) |
| 8 | (11,18) |
| 9 | (12,20) |
威佐夫博弈的结论
仔细观察上表,可以得出以下几个规律。
(1)状态是单调递增的(废话)
(2)状态的石子数量的差是个等差数列(公差为1),这个序列为:0,1,2,3,4,5,6,7,8,9,10,11……
(3)状态的第一个数字是之前没有出现过的第一个数字。比如说第二个状态的第一个数字1,就是前几个状态没有出现的数字。
(4)每个状态的第一个数字竟然是这个状态的两堆石子数量的差$*1.618$
关于$1.618$
$1.618$是一个非常神奇的数字,它既是黄金分割率的近似值+1,即$0.618+1$,也是$(\sqrt{5}+1)/2$,即$(\sqrt{5}+1)/2 \approx 1.618$。
有图为证:
——转自百度百科
但是为什么众多OIer在打威佐夫博弈时不直接使用1.618呢,因为C++/Pascal有一个奇妙的东西——精度
解决洛谷的P2252 取石子游戏
这道题就是裸的威佐夫博弈啊。。。
不多说了,上代码:
1 | int main(){ |
是不是感觉有点乱。。。QWQ
简洁的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27#include<bits/stdc++.h>
using namespace std;
inline int read(){
char ch=getchar();int res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
int a,b;
int main(){
a=read();b=read();
if(a==b){
puts("1");
return 0;
}
if(a==0||b==0){
puts("1");
return 0;
}
int x=min(a,b),y=max(a,b);
double r=(sqrt(5.0)+1.0)/2.0;
double c=(double)(y-x);
int tmp=r*c;
if(tmp==x) puts("0");
else puts("1");
return 0;
}
Link Cut Tree 学习笔记[更新中]
学习动态树$LCT$之前必须要学习$Splay$。。。
Splay 学习笔记[更新中]
这是学习$LCT$的大前提,然而这种树基于一个叫做二叉搜索树$(Binary Search Tree)$的东西,它可以支持平均$O(logN)$的查找、插入、删除等操作。二叉搜索树的任何子树满足一个条件:左儿子比根节点小,右儿子比根节点大,任何一个节点的左子树的所有节点权值都小于这个节点,右子树的所有节点权值都小于这个节点。。但是“平均”一词在$OI$中是…你懂的,世界上有万万千千个出题人来卡掉它。就比如说这棵树:

如果出题人很恶毒换了一种输入顺序:

那么你就会惊奇的发现:你辛辛苦苦打的二叉搜索树退化成了一条链,它的时间复杂度从优秀的$O(logN)$退化成了$O(N)$。
这个时候,奆佬$Tarjan$帅气出场,对对对,就是他发明了Splay让我们多学习一种新算法,这位奆佬还发明了一堆图论算法和数据结构,证明了一堆结论。
fhq treap 学习笔记
序
今天心血来潮,来学习一下fhq treap(其实原因是本校有个OIer名叫fh,当然不是我)
简介
fhq treap 学名好像是“非旋转式treap及可持久化”。。。听上去怪怪的。其实就是可以代替LCT、BST等等码量很高的东东。
定义
1 | struct node{ |
操作
最基本的操作
其实都不应该叫做操作。应该类似于维护的。。。1
2
3
4
5
6
7
8
9
10void update(int x){
tr[x].sz=tr[tr[x].son[0]].sz+tr[tr[x].son[1]].sz+1;//更新节点个数,将左右子树节点个数+本节点(不要忘了。。QWQ)
}
int new_node(int v){
tot++;//总节点编号++
tr[tot].sz=1;//默认为1(叶子)
tr[tot].val=v;//权值赋值
tr[tot].rand_val=rand();//随机rand权值
return tot;//返回节点编号
}
基本操作
其实就三个啦。。。。
操作1:merge(默认x<y)
merge的操作其实就是把两棵树合并成一棵(真好!)。使用递归。按照rand出来的权值进行判断是左子树还是右子树。1
2
3
4
5
6
7
8
9
10
11
12int merge(int x,int y){
if(!x||!y) return x+y;//如果有一棵树是空的,那么就可以直接退出
if(tr[x].rand_val<tr[y].rand_val){//按照rand的权值确定左右子树
tr[x].son[1]=merge(tr[x].son[1],y);//将x的右儿子中merge树y
update(x);//更新节点数
return x;//返回
}else{//同理
tr[y].son[0]=merge(x,tr[y].son[0]);
update(y);
return y;
}
}
操作2:split
split的操作其实就是把一棵树拆成两棵子树。当然有两种拆法,一种是按照权值,还有一种是按照节点数分。
这里的操作2是按照权值分,操作3按照节点数分。1
2
3
4
5
6
7
8void split(int now,int k,int &x,int &y){//以权值k来分now树,成x,y
if(!now) x=y=0;//如果当前操作为空树,返回空子树
else{
if(tr[now].val<=k) x=now,split(tr[now].son[1],k,tr[now].son[1],y);//如果小于或等于权值k,将左子树改为当前的树,并将当前的树的右子树继续往下分(把所有小于等于权值k的节点划分到一棵树当中)
else y=now,split(tr[now].son[0],k,x,tr[now].son[0]);//同理
update(now);//注意更新节点数
}
}
操作3:rank
在操作2中已经说明过了,是按照节点数分(有点像其他数据结构中查找第k名的操作)1
2
3
4
5
6
7
8
9
10
11
12int rank(int now,int k){//在now树中,查找以权值排序的第k个节点
while(1){
if(k<=tr[tr[now].son[0]].sz) now=tr[now].son[0];//如果k在左子树当中那就更新
else{
if(k==tr[tr[now].son[0]].sz+1) return now;//正好找到
else{//如果k在右子树当中,注意k还要减去左子树的个数+本节点
k-=tr[tr[now].son[0]].sz+1;
now=tr[now].son[1];
}
}
}
}
普通的操作
拿一道例题来讲吧。。。
传送门
其实操作并没有高级多少(主要是想象力。。。)
操作1:插入$x$数
1 | split(root,a,x,y); |
这个比较好理解,我们先把树分为x,y两部分,然后把新的节点a看做是一棵树,先与x合并,合并完之后将合并的整体与y合并
操作2:删除$x$数(若有多个相同的数,因只删除一个)
1 | split(root,a,x,z); |
首先我们把树分为x和z两部分
那么x树中的最大权值为a
再把x分为x和y两部分。
此时x中的最大权值为a-1,且权值为a的节点一定是y的根节点。
然后我们可以无视y的根节点,直接把y的左右孩子合并起来,这样就成功的删除了根节点,
最后再把x,y,z合并起来就好
操作3:查询$x$数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数,因输出最小的排名)
1 | split(root,a-1,x,y); |
我们首先按照a-1的权值把树分开。
那么x树中最大的应该是a-1。
那么a的排名就是siz[x]+1
操作4:查询排名为$x$的数
//rank函数不是白吃饭的1
printf("%d\n",tr[rank(root,a)].val);
不解释了QWQ
操作5:求$x$的前驱(前驱定义为小于$x$,且最大的数)
//rank函数真的不是白吃饭的1
2
3split(root,a-1,x,y);
printf("%d\n",tr[rank(x,tr[x].sz)].val);
root=merge(x,y);
因为要小于a,那么我们按照a-1的权值划分,
x中最大的一定是<=a-1的,
所以我们直接输出x中最大的数就好,
(这里有一个小技巧,因为sz储存的是节点的数目,然后根据二叉查找树的性质,编号最大的就是值最大的)
操作6:求$x$的后继(后继定义为大于$x$,且最小的数)
//rank函数真的不是白吃饭的1
2
3split(root,a,x,y);
printf("%d\n",tr[rank(y,1)].val);
root=merge(x,y);
因为要大于a,那么我们按照a的权值划分(取子树y),
y中最小的一定是>a的,
所以我们直接输出y中最小的数就好,
(像操作5一样这里有一个小技巧,因为sz储存的是节点的数目,然后根据二叉查找树的性质,编号最小的就是值最小的)
完整的代码:
1 | #include<bits/stdc++.h> |
写在最后
当然,fhqtreap的应用不仅限于这些,还有许多,还待我继续学习。。。
Codeforces Round 536 (Div. 2)游记
2019.1.31
一次难得的中国场,时间还是在$20:30$,虽然说打到一半,公告$unrated$了,虽然说打到一半$in$ $queue$上$200$页了,但本蒟蒻还是打了下去(都是泪呀)。
说一说比赛概况吧。。。
丑陋的水印↑。
被xryjr233虐了。。。
你没看错,rnk1的rqy被我抠了。。。
扯完了,来看一下题目:
A. Lunar New Year and Cross Counting
题意
给一个$n\times n$的矩阵,这个矩阵由$X$和$.$组成,问在这个矩阵内有多少个图案:1
2
3X.X
.X.
X.X
$1\leq n \leq 500$
思路
暴力就好了鸭,但是比赛时不知道哪里打错了。。。交了3次, 都是泪鸭。。。
都是泪鸭。。。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21#include<bits/stdc++.h>
using namespace std;
char a[710][710];
int n,ans=0;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(a[i][j]=='X'&&a[i-1][j-1]=='X'&&a[i-1][j+1]=='X'&&a[i+1][j-1]=='X'&&a[i+1][j+1]=='X'){
ans++;
}
}
}
cout<<ans<<endl;
return 0;
}
B. Lunar New Year and Food Ordering
题意
一开始,餐厅里有$n$种菜,第$i$种菜有$a_i$份,每份$c_i$元。
现在时除夕夜,有$m$个顾客要来吃饭,第$i$个顾客吃$t_i$种$d_i$份。
如果不够,就补最便宜的,如果真的不够,那么就走人(支付$0$元,但还是吃了部分)
思路
模拟就好了。。。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36#include<bits/stdc++.h>
#define E 100010
#define ll long long
#define Orz 998244353
using namespace std;
ll n,m,kkk;
struct node{
ll has,cost,id;
}a[E];
ll f[E];
bool cmp(node qx,node qy){
return qx.cost<qy.cost||(qx.cost==qy.cost&&qx.id<qy.id);
}
int main(){
cin>>n>>m;
for(ll i=1;i<=n;i++) cin>>a[i].has;
for(ll i=1;i<=n;i++) cin>>a[i].cost,a[i].id=i;
sort(a+1,a+n+1,cmp);
for(ll i=1;i<=n;i++){
f[a[i].id]=i;
}
kkk=1;
for(ll i=1;i<=m;i++){
ll ci,cn;
cin>>ci>>cn;
if(kkk>n) puts("0");
else{
ll ans=0;
ll bn=min(cn,a[f[ci]].has);
ans+=1ll*a[f[ci]].cost*bn,cn-=bn,a[f[ci]].has-=bn;
if(cn) while(kkk<=n&&cn) bn=min(cn,a[kkk].has),cn-=bn,a[kkk].has-=bn,ans+=1ll*a[kkk].cost*bn,kkk+=(a[kkk].has==0);
cout<<(cn?0ll:ans)<<endl;
}
}
return 0;
}
C. Lunar New Year and Number Division
题意
将$n$个数字,分成$m$组,使得每一组的数字之和的平方之和最小。
问这个最小值是多少。$n$是偶数。$m$是任意数。
思路
肯定是两两一组啦。。。至于最小嘛肯定是一大一小一组。贪心。
设这$n$个数字为$a_1,a_2,a_3,a_4…a_{n-1},a_n$(按从小到大顺序排列),那么贪心的最小值为:
$$(a_1+a_n)^2+(a_2+a_{n-1})^2…(a_{n/2}+a_{n/2+1})^2$$
即:
$${a_1}^2+{a_2}^2+…{a_n}^2+2\times a_1 \times a_n+2\times a_2 \times a_{n-1}…+2\times a_{n/2}\times a_{n/2+1}$$
因为${a_1}^2+{a_2}^2+…{a_n}^2$是不会变的(更改位置后)
所以只需要比较$\times a_1 \times a_n+2\times a_2 \times a_{n-1}…+2\times a_{n/2}\times a_{n/2+1}$的大小即可,而$2\times a_1 \times a_n+2\times a_2 \times a_{n-1}…+2\times a_{n/2}\times a_{n/2+1}$的最小值必定是$2\times$一大一小(我懒,不证明了),所以最小值肯定为$(a_1+a_n)^2+(a_2+a_{n-1})^2…(a_{n/2}+a_{n/2+1})^2$。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a[300010];
ll n,ans=0;
int main(){
cin>>n;
for(ll i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
for(ll i=1;i<=n/2;i++){
ans+=(a[i]+a[n-i+1])*(a[i]+a[n-i+1]);
}
cout<<ans<<endl;
return 0;
}
D. Lunar New Year and a Wander
题意
求一个无向图的字典序最小的遍历。
思路
因为每个点是可以走重复的,所以肯定使用$bfs$,而又因为是字典序最小的,所以使用堆$priority_queue$,如果本节点确认后就拓展其他相邻的节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38#include<bits/stdc++.h>
#define E 200010
using namespace std;
int n,m;
vector<int> v[E];
int vis[E];
int tt[E];
priority_queue<int,vector<int>,greater<int> > q;
void bfs(int x){
while(!q.empty()) q.pop();
memset(vis,0,sizeof(vis));
memset(tt,0,sizeof(tt));
q.push(x);
while(!q.empty()){
int u=q.top();q.pop();
if(vis[u]==0){cout<<u<<" ";
vis[u]=1;
for(int i=0;i<v[u].size();i++){
int to=v[u][i];
q.push(to);
}}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
for(int i=1;i<=n;i++){
sort(v[i].begin(),v[i].end());
}
bfs(1);
return 0;
}
E. Lunar New Year and Red Envelopes
题意
留个坑以后再填
思路
留个坑以后再填
F. Lunar New Year and a Recursive Sequence
题意
留个坑以后再填
思路
留个坑以后再填
10202. 「一本通 6.2 练习 5」樱花
题意
求不定方程:
$$
\frac{1}{x}+\frac{1}{y}=\frac{1}{n!}
$$
的正整数解 $(x,y)$ 的数目。
思路
$$
\frac{1}{x}+\frac{1}{y}=\frac{1}{n!}
$$
$$
\frac{y}{xy}+\frac{x}{xy}=\frac{1}{n!}
$$
$$
\frac{x+y}{xy}=\frac{1}{n!}
$$
$$
n!\times(x+y)=xy
$$
$$
x+y=\frac{xy}{n!}
$$
$$
(x-n!)*(y-n!)=(n!)^2
$$
1 | #include<bits/stdc++.h> |
10184. 「一本通 5.6 例 1」任务安排 1 & 10185. 「一本通 5.6 例 2」任务安排 2 & 10186. 「一本通 5.6 例 3」任务安排 3
由于这三道题都是同一道题,只是数据范围不同,故拉成同一篇博客
题意
有$n$个任务,机器人($jxc$)会把这$n$个任务分成若干批,从时刻$0$开始,任务将被分批加工,执行第$i$个任务需要花费时间为$T_i$。另外,在每一批任务开始前,机器需要$S$的启动时间。
同一批任务将在同一时刻完成。每个任务的费用$=$它完成的时间$\times$一个费用的系数$C_i$。
思路
对于$n \leq 5000$的数据
时间复杂度$O(N^2)$
设$f[i]$表示前$i$个任务所花费最小价值。
初始化:
$$f[i]=inf|1<=i<=n,f[0]=0$$
转移方程:
$$f[i]=min \left{f[j-1]+S(c[n]-c[j-1])+t[i](c[i]-c[j-1])|1<=j<=i \right}$$
1 | #include<bits/stdc++.h> |
对于$1\leq N \leq 10^4$的数据
时间复杂度约为$O(N)$
转移方程同上,
$$f[i]=min \left{ f[j-1]+S(c[n]-c[j-1])+t[i](c[i]-c[j-1])|1<=j<=i \right }$$
将只含有$i$的项移出,得:
$$f[i]=min \left { f[j-1]-Sc[j-1]-t[i]c[j-1]|1<=j<=i \right }+Sc[n]+t[i]c[i]$$
合并同类项,得:
$$f[i]=min \left { f[j]-(S+t[i])c[j]|0<=j<=i-1 \right }+Sc[n]+t[i]*c[i]$$
设$y=f[j]$,$k=S+t[i]$,$x=c[j]$,$b=Sc[n]+t[i]c[i]$
那么:
$$f[i]=y-kx+b$$
即:
$$y=kx+(f[i]-b)$$
斜率优化一:
因为$t[i]$在递增,斜率$k$在变大,直线越来越陡,所以队首的两个点之间斜率至少要大于$(S+t[i])$。
即:$(f[q[l+1]]-f[q[l]])/(c[q[l+1]]-c[q[l]])>(S+t[i])$
即:若$(f[q[l+1]]-f[q[l]])/(c[q[l+1]]-c[q[l]])<=(S+t[i])$,队首弹出
化简,得:若$(f[q[l+1]]-f[q[l]])<=(S+t[i])*(c[q[l+1]]-c[q[l]])$,队首弹出斜率优化二:
确保右侧的斜率大于左侧的斜率,即:$(f[q[r]]-f[q[r-1]])/(c[q[r]]-c[q[r-1]])<(f[i]-f[q[r]])/(c[i]-c[q[r]])$。
若$(f[q[r]]-f[q[r-1]])/(c[q[r]]-c[q[r-1]])>=(f[i]-f[q[r]])/(c[i]-c[q[r]])$,队尾弹出。
化简,得:若$(f[i]-f[q[r]])(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])(c[i]-c[q[r]])$,队尾弹出
1 | #include<bits/stdc++.h> |
对于$1 \leq N \leq 3 \times 10^5 , \left| T_i \right|<2^8$的数据
虽然添加了单调队列的优化,但是时间可以为负数,所以之前维护的单调性就不存在了,所以我们需要使用二分+单调队列来维护斜率。
1 | #include<bits/stdc++.h> |
10175. 「一本通 5.5 例 1」滑动窗口
题意
给一个长度为 $N$ 的数组,一个长为 $K$ 的滑动窗体从最左端移至最右端,你只能看到窗口中的 $K$ 个数,每次窗体向右移动一位,你的任务是找出窗体在各个位置时的最大值和最小值。
思路
DP水过去。。。
加上优先队列优化。。。
1 | #include<bits/stdc++.h> |


